Schmelzer wrote:It is a prediction of standard QM that in this case

holds.
QM takes for granted that the measurement is simultaneous (aka at the same time) since both particles are described by the same wavefunction evolving in time. Therefore

, is perfectly consistent with QM
 = - B_a(\psi))
. It is not my problem if Bell is sloppy and ignores that fact. Sorry there is no contradiction with QM to see here, move on to something else.
Schmelzer wrote:So, if the experiment would observe something different, QM would have been falsified and everybody would be happy about new physics to explore.
 = - B_a(\lambda, t_6))
is perfectly consistent with the QM prediction of
 = - B_a(\psi))
when t_3 = t_6. Besides, if you claim that

is arbitrary and can be anything, then

should also contain time within it, so when you see
 = - B_a(\lambda))
, it means precisely that the

at Alice has exactly the same value as that at Bob, which implies measurement at the exact same time! All I've done is separate out the time from your "arbitrary"

, to tickle your imagination into realizing that the measurement must be at the same time. There is no new physics to explore here, just a lack of imagination on the part of Bell and his followers, to realize the simple fact that for time dependent hidden variables or functions, leaving out time does not give you a complete specification. If time is included in

, then the measurement time must be exactly the same on both sides. Sorry there is no falsification of QM to see here, move on to something else.
Schmelzer wrote:Given that the two measurements are space-like separated, we can always choose a time coordinate such that the two measurements happen at the same "time". So, not only quantum theory would be falsified, relativity would be falsified too, with the different result

for equal "true time" and

otherwise.
Utter Garbage. Don't tell me you have problems understanding relativity too?

When you write
 = - B_a(\lambda))
, it is understood mathematically that the

on both sides means exactly the same thing. You want to use a different basis to define

each side, you may as well write
 = - B_a(\zeta))
. There is no way to predict at
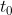
, the outcome of a measurement governed by a time dependent function, if you do not know at what time it will be measured. Picking a different basis in order to have the same
value, does not give you the same
meaning. If I tell you Bob has measured his particle, there is no way Alice would be able to tell what outcome Bob would have gotten unless she knew exactly at what time Bob measured the particle, and if you are playing dirty tricks with time coordinates, Alice would have to know both the time value, and the time coordinate, in order to calculate the outcome of Bob. So sorry, there absolutely is no conflict with relativity here, and no conflict with QM here. Move on to something else.
minkwe wrote:The ensembles of

used to calculate the correlations must be identical for each term. If

is time dependent, that means everything must be done at the same times, which is not a problem for counterfactual outcomes which are fully theoretical. But impossible for actual experiments.
Once, following the EPR argument, the results are predetermined, and fixed by

, it does not matter at all at which moment one actually measures them.
The EPR argument says:
EPR wrote:if, without in any way disturbing a system, we can predict with certainty (ie, with probability equal to unity) the value of a physical quantity, then there exists an element of physical reality corresponding to this physical quantity
.
For time dependent functions, there is no way to predict with certainty what the value would be, unless you know at what time it would be measured. You can't have it both ways. Either you include the measurement time in

in order to be able to predict with certainty, (and assume they are the same on both sides), or you don't have a complete specification according to EPR. So sorry, there is no conflict between what I'm saying and the EPR argument. Move on to something else.
Schmelzer wrote:That's an interesting new technique. Introducing multiple nonsense, and, if the opponent focusses his interest on only one, the most horrible nonsense, then accusing him of not having seen the other nonsense.

There is no nonsense in what I've argued. The person spouting nonsense is the one who claimed: "there is no CFD in QM" only to backtrack later that "yes, we have CFD in QM, in some exceptional cases". The person who claimed that the outcome of a measurement governed by a time dependent function can be predicted with certainty at
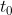
without knowledge of the measurement time, is the one who has been spouting nonsense. If only they are paid more careful attention, they would have avoided the embarrassment of having to retract yet another stupid claim.
Schmelzer wrote:I have long searched for a meaningful interpretation and finally found one for
,\lambda, t_0))
as a way of denoting with

that A is measured at the time

,
)
as denoting that a is chosen at time
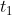
, and the
)
as that the values of

and the function A(...) are those taken at time
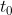
.
But, ok, I acknowledge that the attempt to make sense of your formulas was false. I should not have tried to give your formulas a meaningful interpretation and to try to follow your challenge to prove something with them, but should have immediately rejected them as as a meaningless mixture of letters.
I've told you already, nobody gives a rat's behind at what time the settings were chosen. The settings are fixed for a given P(a,c). The only thing that matters is the time at which the
outcomes were obtained.
Outcomes, because the inequalities are about
outcomes, and because experimental tests calculate averages from
outcomes. If you ignore the physics of the experiment under consideration, you end up in lalaland.
, A(a, \lambda, t_1), A(a, \lambda(t_1)), A_a(\lambda(t_1)))
Are all equivalent notations to reflect the fact that the outcome of the function is time dependent, and evaluated at time
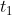
. I haven't introduced any new symbols here. If those symbols appear to you to be meaningless mixtures of letters, you should probably consider moving to fishing for a new profession.
Bottom line:
1) There is no locality assumption required to in the derivation inequalities, despite claims (See de Raedt et al, and Rosinger's paper for details).
2) The CFD assumption, required to derive the inequalities also applies to QM
3) The use of counterfactual outcomes in the inequalities precludes experimental tests
4) Either the inequalities forbid time dependent functions
, B(t))
or time dependent hidden variables
)
, or they require that all measurements be performed at the same time.
Each of these points by itself is fatal to Bell's theorem but together, they simply shatter it to smithereens. No reasonable person can continue to Believe Bell's theorem is true.
We can therefore mirror Bell's own words against von Neuman toward him:
It was not the objective measurable predictions of quantum mechanics which ruled out hidden variables. It was the arbitrary assumption of a particular (and impossible) relation between the results of incompatible measurements either of which might be made on a given occasion but only one of which can in fact be made.Yet the Bell proof, if you actually come to grips with it, falls apart in your hands! There is nothing to it. It’s not just flawed, it’s silly. If you look at the assumptions it made, it does not hold up for a moment. It’s the work of a mathematician, and he makes assumptions that have a mathematical symmetry to them. When you translate them into terms of physical disposition, they’re nonsense. You may quote me on that: the proof of Bell is not merely false but foolish.
