A new simulation of the EPR-Bohm correlations

[Jochen]

OK, so what do you do with the events in which A(a,e,s)=0?

There are no such events. Please read through the simulation carefully. You will see what I mean.

Nope, sorry. There certainly are cases for which the formula yields zero. No? So then you say 'those don't exist in '. But what's that supposed to mean? If Alice sets her device to an a such that for given (e,s) A(a,e,s)=0, does she then simply not observe an event, even though the source produces a particle? Then there's no fair sampling. Can she not set her measuring apparatus to a? Then there is no full freedom. Does the source not send out the particle pair? Then there is non-locality, as whether or not the source sends out particles depends on Alice's detector setting. So what is the physical interpretation of those cases in the simulation where A(a,e,s)=0?

[Joy Christian]

OK, so what do you do with the events in which A(a,e,s)=0?

There are no such events. Please read through the simulation carefully. You will see what I mean.

Nope, sorry. There certainly are cases for which the formula yields zero. No? So then you say 'those don't exist in '. But what's that supposed to mean? If Alice sets her device to an a such that for given (e,s) A(a,e,s)=0, does she then simply not observe an event, even though the source produces a particle? Then there's no fair sampling. Can she not set her measuring apparatus to a? Then there is no full freedom. Does the source not send out the particle pair? Then there is non-locality, as whether or not the source sends out particles depends on Alice's detector setting. So what is the physical interpretation of those cases in the simulation where A(a,e,s)=0?

Please try to suspend your prejudices for just a few minutes. Please read through the simulation. Note that S^3 is defined by the metric {g, t}. What does that metric dictate? There are no occasions where Alice sets her device to an a for which A(a,e,s) = 0, because the corresponding state (e,s) simply does not exist in S^3. You cannot observe something that is not there in the first place. She can certainly set her measuring apparatus to any direction a or a' she likes, and she will indeed observe events for all directions, but she will not observe anything if the source has not produced anything. There is one-to-one correspondence between the states w = (e,s) within S^3 and the events A and B observed by Alice and Bob. There are no cases where A(a,e,s) = 0 for the states w=(e,s) belonging to S^3. None whatsoever.

As I noted before, in my 3-sphere model measurements always yield a result. All detectors in the model are of 100% efficiency. The data obtained is a fair sample of the data produced. No data has been rejected based on the measurement direction. Every single initial state (e,s), or particle w, is detected. There is one-to-one correspondence between the initial states w = (e,s) and the measurement results A and B. Both CHSH and CH inequalities are duly "violated", since all 13 probabilistic predictions of the model match exactly with the corresponding predictions of quantum mechanics. Bell's theorem has thus been put to rest, and constructively so, not just formally. The only reason you seem not to recognize this is because you seem to be stuck in R^3. But we do not live in R^3. We live in S^3. That is the model.

To this I add that there is no compromise in the model with the experimenter's freedom to choose whatever directions she likes. Please read my papers I have linked.

[Jochen]

Please try to suspend your prejudices for just a few minutes. Please read through the simulation. Note that S^3 is defined by the metric {g, t}. What does that metric dictate? There are no occasions where Alice sets her device to an a for which A(a,e,s) = 0, because the corresponding state (e,s) simply does not exist in S^3. You cannot observe something that is not there in the first place. She can certainly set her measuring apparatus to any direction a or a' she likes, and she will indeed observe events for all directions, but she will not observe anything if the source has not produced anything.

But let's take a look at a single event. The source produces a particle pair corresponding to the HV-state (e,s). Now, there exist measurement directions a for which Alice will either observe +1 or -1. If she chooses one of these directions---after the source has produced the particle pair, and hence, after the HV state has been fixed---then everything will be fine, and she records the proper observation. But what if she, again after the HVs have been fixed, chooses a measurement direction such that A(a,e,s)=0? Is she prohibited from doing this? Does she fail to make an observation? What happens in this case?

[Joy Christian]

Please try to suspend your prejudices for just a few minutes. Please read through the simulation. Note that S^3 is defined by the metric {g, t}. What does that metric dictate? There are no occasions where Alice sets her device to an a for which A(a,e,s) = 0, because the corresponding state (e,s) simply does not exist in S^3. You cannot observe something that is not there in the first place. She can certainly set her measuring apparatus to any direction a or a' she likes, and she will indeed observe events for all directions, but she will not observe anything if the source has not produced anything.

But let's take a look at a single event. The source produces a particle pair corresponding to the HV-state (e,s). Now, there exist measurement directions a for which Alice will either observe +1 or -1. If she chooses one of these directions---after the source has produced the particle pair, and hence, after the HV state has been fixed---then everything will be fine, and she records the proper observation. But what if she, again after the HVs have been fixed, chooses a measurement direction such that A(a,e,s)=0? Is she prohibited from doing this? Does she fail to make an observation? What happens in this case?

I presume you mean a state (e,s) within S^3, which is equivalent to a vector w (as explained in the recently augmented version of the simulation).

For a direction a Alice will observe A(a, w) = -sign(a.w) = +1 or -1.

For a direction a' Alice will observe A(a', w) = -sign(a'.w) = +1 or -1. And so on.

There are no directions a for which A(a, w) = 0. Alice is free to choose any direction "a" she likes. Whatever direction "a" she chooses, she will observe either +1 or -1.

[Jochen]

There are no directions a for which A(a, w) = 0. Alice is free to choose any direction "a" she likes. Whatever direction "a" she chooses, she will observe either +1 or -1.

But there are, for any (e,s), directions a such that A(a,e,s) = 0. Right?

[Joy Christian]

There are no directions a for which A(a, w) = 0. Alice is free to choose any direction "a" she likes. Whatever direction "a" she chooses, she will observe either +1 or -1.

But there are, for any (e,s), directions a such that A(a,e,s) = 0. Right?

Yes, but those (e,s) do not belong to S^3. You still haven't read the simulation or the theoretical paper.

The situation is analogous to what happens in gauge theory. You have a pre-phase space, with gauge dependent vector potential etc. Then, in the physical or reduced phase space, all quantities are gauge invariant or gauge independent. Similarly, in my model there are no states w = (e,s) within S^3 such that A(a,e,s) = 0 within S^3.

[Jochen]

There are no directions a for which A(a, w) = 0. Alice is free to choose any direction "a" she likes. Whatever direction "a" she chooses, she will observe either +1 or -1.

But there are, for any (e,s), directions a such that A(a,e,s) = 0. Right?

Yes, but those (e,s) do not belong to S^3. You still haven't read the simulation or the theoretical paper.

But what does belong to S^3 and what doesn't is then dependent on Alice's measurement setting. Looking at (e,s) alone does not suffice to tell whether it 'belongs to S^3', or not?

[Joy Christian]

But what does belong to S^3 and what doesn't is then dependent on Alice's measurement setting. Looking at (e,s) alone does not suffice to tell whether it 'belongs to S^3', or not?

No, the structure of S^3 is no more dependent on Alice's choice of measurement setting than the structure of R^3 is.

The structure of S^3 is determined by the metric {g, t}, which is defined for any pair of vectors (u,v), as any such inner product is defined in Riemannian geometry.

This is much more evident in the Clifford-algebraic representation of the 3-sphere: http://arxiv.org/abs/1501.03393 [cf. Eq. (B10)].

[minkwe]

So if there is no joint PD, then local realism doesn't hold.

You've conveniently ignored the following argument which debunked that claim already. It is not always possible to reconstruct a joint PD from experimental data measured in pairs, even if the model is local realistic!

The expression means that for every single individual pair of particles in the series which produced the outcome pair , there is an equivalent pair of particles in the series. This means a function exists which maps a specific particle pair in set , to a specific particle pair in set . Let us call that function . Similarly, ... there must exist other independent functions , , , , , . etc.

Imagine a spreadsheet with two columns labelled , and containing all the outcomes for the series of measurements on its rows. Now let us try to apply the function so that we can place the outcomes from the series of measurements on the next two columns, and we must be able to apply all those functions to all the measurement outcomes and at the end all the columns labelled with similar upper case letters must be identical in numbers of +1's and -1's, and also in the pattern of switching back and forth. Only then can you assume that are all true and the upper bound of 2 should apply.

Can be factored if we apply our mapping functions such that the series of equivalent outcome sequences have the same numbers of +1's and -1's and the same pattern of occurences of those numbers. That is, for the above expression we can use our functions to generate new sequences of outcomes from measured data such that and , where the prime , represents the fact that the sequence of outcomes has been rearranged using the mapping function. Thus we have


With our new re-ordered sets of outcomes we invoke the equivalence and do the factorization to get


But then we immediately face a wall. For this expression to obey the inequality , we also need to be able to rearrange so that and which is for all practical purposes impossible. Note that both and have already been rearranged independently of each other, and since any rearrangement will shuffle both outcomes in the set of pairs, any new rearrangement to make agree with will undo the previous rearrangements. The same for and . Different independent and conflicting rearrangements are required to make the inequality work for 4 separate sets of paired outcomes.

Therefore it is simply not true that the inequality
Derived assuming a single set of quartets of outcomes , should Should apply to 4 different independent sets of pairs of outcomes

This characterizes the state fully to be , i.e. the state is maximally entangled between Alice and Bob, respectively between Cindy and Dave, and completely uncorrelated between the A-B and C-D pairs. Thus, correlations , while . Hence, , and there is no CHSH violation predicted by QM.

1) The derivation of the CHSH starts as follows: . Where A,B,C,D represent measurements on a single pair of spin-half particles. This is exactly equivalent to having two 4 particles in which , where the particle pair used to measure the CD term is identical to the particle pair used to measure AB, just like I describe. An expression like the CHSH inequality was derived precisely by assuming the exact scenario my friends now say is meaningless in QM! The expectation values in the final CHSH expression represents exactly the ones <AB> <AD>, <CB>, <CD>, which the bell believers now either claim QM can not make predictions for, or two of them must be zero

2) The question I asked them about 4 particles, is exactly the same question Bell asked himself in proving the celebrated Bell's theorem. What predictions does QM make for the expectation values <AB> <AD>, <CB>, <CD> in the CHSH expression According to our esteemed guest, the answer is . Now please tell me how this can ever violate the inequality. You see, Bell's followers don't even realize that they believe contradictory things at the same time.

I see that Bell theorem believers like repeating arguments that have already been thoroughly debunked. So please Jochen, there is just one question left:

For the CHSH inequality

Could you please tell us what Quantum Mechanics predicts for the 4 expectation values ?

[Jochen]

But what does belong to S^3 and what doesn't is then dependent on Alice's measurement setting. Looking at (e,s) alone does not suffice to tell whether it 'belongs to S^3', or not?

No, the structure of S^3 is no more dependent on Alice's choice of measurement setting than the structure of R^3 is.

Well, so you claim, but according to your model, for a given HV-state (e,s), the choice of whether it belongs to S^3 is only made once the experimenter chooses her measurement direction. If she chooses an a such that A(a,e,s) = +/-1, then (e,s) belong to S^3, if she chooses an a such that A(a,e,s) = 0, then (e,s) does not belong to S^3. Is that not the case?

[Jochen]

You've conveniently ignored the following argument which debunked that claim already. It is not always possible to reconstruct a joint PD from experimental data measured in pairs, even if the model is local realistic!

This is wrong: I have given an explicit construction such that for any LHV-model, you can construct a joint PD.

Could you please tell us what Quantum Mechanics predicts for the 4 expectation values ?

As such, the question is meaningless. You could ask 'What does Quantum Mechanics predict for the 4 expectation values if the measurements are carried out on a singlet state, and the measurements are those in the standard CHSH setting?', in which case the prediction would be , m and , respectively; but in different settings, wildly different outcomes are possible. Does that help?

[Joy Christian]

But what does belong to S^3 and what doesn't is then dependent on Alice's measurement setting. Looking at (e,s) alone does not suffice to tell whether it 'belongs to S^3', or not?

No, the structure of S^3 is no more dependent on Alice's choice of measurement setting than the structure of R^3 is.

Well, so you claim, but according to your model, for a given HV-state (e,s), the choice of whether it belongs to S^3 is only made once the experimenter chooses her measurement direction. If she chooses an a such that A(a,e,s) = +/-1, then (e,s) belong to S^3, if she chooses an a such that A(a,e,s) = 0, then (e,s) does not belong to S^3. Is that not the case?

No, that is most certainly not the case. I don't know where do you see anything like that in the simulation or in the model. The structure of S^3 is defined by the metric {g, t}, which in turn defines an inner product for any pair of vectors {u, v}, as is usually done in geometry. Appearances of "a" and "e" are then incidental.

It is also important not to forget that a simulation is not a model; it is an implementation of a model. The analytical model is explained in papers I have linked above.

But if you prefer to read only the simulation, then you have to read it in full, not sporadically as you seem to be doing. In the simulation the structure of the 3-sphere is constructed from the background structure of M and e, based on the usual concepts of vector etc. in R^3. This structure is then used to calculate the correlation in a loop within a loop. This calculation must respect the metrical structure of S^3 specified before the loops. So I fail to see how you can infer what you are inferring even if you choose to look only at the simulation. Where in the Eq. (B10) of this paper do you see any dependence of s^k on the choices of measurement directions???

[Jochen]

No, that is most certainly not the case. I don't know where do you see anything like that in the simulation or in the model. The structure of S^3 is defined by the metric {g, t}, which in turn defines an inner product for any pair of vectors {u, v}, as is usually done in geometry. Appearances of "a" and "e" are then incidental.

Well, OK, so what's wrong about this story: first, (e,s) are determined. Then, A chooses a measurement direction a. If things are such that A(a,e,s) = +/-1, then she will observe either +1 or -1. If things are such that A(a,e,s) = 0, then she will not make any observation. Is that correct?

But if you prefer to read only the simulation, then you have to read it in full, not sporadically as you seem to be doing.

I care about replicating the actual observations an experimenter makes in your model. As best I can tell, I have done so. From an operational point of view, that's all there is to the model.

[Joy Christian]

No, that is most certainly not the case. I don't know where do you see anything like that in the simulation or in the model. The structure of S^3 is defined by the metric {g, t}, which in turn defines an inner product for any pair of vectors {u, v}, as is usually done in geometry. Appearances of "a" and "e" are then incidental.

Well, OK, so what's wrong about this story: first, (e,s) are determined. Then, A chooses a measurement direction a. If things are such that A(a,e,s) = +/-1, then she will observe either +1 or -1. If things are such that A(a,e,s) = 0, then she will not make any observation. Is that correct?

I can see why you would like it to be correct, but it is not correct.

The correct story is this:

First, the initial state w = (e,s) emeges from the source within S^3.

Then, Alice chooses a measurement direction a.

Then her detector computes -sign(a.w) and gets the result A(a,w) = +/-1.

End of the story (as far as Alice is concerned).

But if you prefer to read only the simulation, then you have to read it in full, not sporadically as you seem to be doing.

I care about replicating the actual observations an experimenter makes in your model. As best I can tell, I have done so. From an operational point of view, that's all there is to the model.

What you have done is produce your own model that has nothing much to do with my model. But we are now seem to be going in circles, so I will stop there.

[minkwe]

The simulation is intended to argue that local realistic models can violate Bell inequalities, but it misses its mark, in violating a Bell inequality that would not be expected to hold in this scenario anyway, since one needs a higher detection efficiency than you provide in order to perform a conclusive test.

Did you forget what Bell said:

In a theory in which parameters are added to quantum mechanics to determine the results of individual measurements, without changing the statistical predictions, there must be a mechanism whereby the setting of one measuring device can influence the reading of another instrument, however remote. Moreover, the signal involved must propagate instantaneously, so that a theory could not be Lorentz invariant.[4]

I suppose then that you have no problem if I fix that for him, by adding in your claims as follows:

In a theory in which parameters are added to quantum mechanics to determine the results of individual measurements, without changing the statistical predictions, it is not necessarily the case that there must be a mechanism whereby the setting of one measuring device can influence the reading of another instrument, however remote. It could be that either not all particles are detected, or it is not always possible to reliably pair detected particles. Therefore, the idea of a signal which must propagate instantaneously, or the idea of a theory that is not Lorentz invariant is premature.

Do you have any problems with that? Because that is essentially what you are arguing! That my simulations are local HV models and can reproduce the QM predictions, but Bell's theorem only applies to models in which all emitted particles are detected and all detected particles can be reliably paired. Bell's followers have perfected the art of goal-shifting.

You've conveniently ignored the following argument which debunked that claim already. It is not always possible to reconstruct a joint PD from experimental data measured in pairs, even if the model is local realistic!

This is wrong: I have given an explicit construction such that for any LHV-model, you can construct a joint PD.

You ignored the argument. I just showed you that you are wrong, where specifically does the argument fail. Please be very specific.

For the CHSH inequality

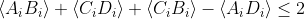
Could you please tell us what Quantum Mechanics predicts for the 4 expectation values ?

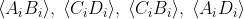
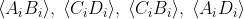
As such, the question is meaningless.You could ask 'What does Quantum Mechanics predict for the 4 expectation values if the measurements are carried out on a singlet state, and the measurements are those in the standard CHSH setting?

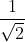
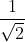
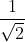
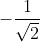
prediction would be , m and , respectively;

You just provided two different QM predictions for the same question. Maybe you haven't realized yet that your previous answer was:


Note that Bell believers don't even agree what the answer should be. Some say a QM prediction is not possible because the scenario is impossible in QM. Other Bell believers simply ignore the stated correlation between A and C, and answer a different question. Either way, the example allows me to show very clearly the duplicity of their beliefs because they now answer that


Perhaps because you haven't yet appreciated the difference between

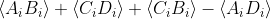
and

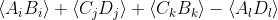
The former is the CHSH, the latter is not. The upper bound of the former is 2, the upper bound of the latter is higher than 2. Please review Adeniers paper if you still do not understand this:
http://arxiv.org/abs/quant-ph/0006014
A Refutation of Bell's Theorem

Bell's Theorem was developed on the basis of considerations involving a linear combination of spin correlation functions, each of which has a distinct pair of arguments. The simultaneous presence of these different pairs of arguments in the same equation can be understood in two radically different ways: either as `strongly objective,' that is, all correlation functions pertain to the same set of particle pairs, or as `weakly objective,' that is, each correlation function pertains to a different set of particle pairs.
It is demonstrated that once this meaning is determined, no discrepancy appears between local realistic theories and quantum mechanics: the discrepancy in Bell's Theorem is due only to a meaningless comparison between a local realistic inequality written within the strongly objective interpretation (thus relevant to a single set of particle pairs) and a quantum mechanical prediction derived from a weakly objective interpretation (thus relevant to several different sets of particle pairs).

I don't think you have appreciated that

could not possibly be the correct QM prediction. Don't you see that the terms in the CHSH are not independent? In fact, what is correct is

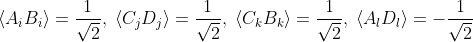
Don't you see that the QM predictions are for independent ensembles of particle pairs. How can Bell's followers argue that if one pair of particles is in an entangled spin-1/2 state, it must be independent from another pair that is also in an entangled spin-1/2 state. But then turn around and shift the goal-post by using completely independent expectation values in an expression which contains terms that are not independent. But since you don't appreciate the difference yet, you substitute the two erroneously.

Nothing can violate the CHSH. The claimed violation is simply due to mathematical fumbles equating apples to oranges. Bell's theorem is nonsense. I don't understand what the mental block could be that is preventing people from seeing what is so clear. There is no paradox, there is no non-locality. Bell's theorem is simply one big mathematical mistake!

[Jochen]

I can see why you would like it to be correct, but it is not correct.

It's what the simulation produces.

The correct story is this:

First, the initial state w = (e,s) emeges from the source within S^3.

Then, Alice chooses a measurement direction a.

Then her detector computes -sign(a.w) and gets the result A(a,w) = +/-1.

End of the story (as far as Alice is concerned).

This story squares neither with your nor my implementation. The function g returns 0 for all orientations of Alice's measurement device that fail the check against the value f, which depends on s. You then erase them from Alice's measurement record by counting only those for which abs(sign(g)) > 0, which is achieved by the function t, invoked by n. A measurement in a direction a such that A(a,e,s) would be zero will thus not occur in the measurement record.

[Joy Christian]

The correct story is this:

First, the initial state w = (e,s) emeges from the source within S^3.

Then, Alice chooses a measurement direction a.

Then her detector computes -sign(a.w) and gets the result A(a,w) = +/-1.

End of the story (as far as Alice is concerned).

This story squares neither with your nor my implementation. The function g returns 0 for all orientations of Alice's measurement device that fail the check against the value f, which depends on s. You then erase them from Alice's measurement record by counting only those for which abs(sign(g)) > 0, which is achieved by the function t, invoked by n. A measurement in a direction a such that A(a,e,s) would be zero will thus not occur in the measurement record.

There are no zero outcomes either in my theoretical model or in its simulation. They simply do not exist. One cannot detect that which is not there in the first place!

To analyze the data, I throw out all the 0-results, and compute the correlation for the four possible settings for the remaining data points

Why do you have to throw away anything in order to calculate

Besides, as evident from both my theoretical model and its simulation, the {0,+}, {0,-}, {+,0}, {-,0}, and {0,0} outcomes simply do not exist within S^3. An elementary fact that flatlanders like Gill are having a great deal of difficulty understanding. One cannot measure, or "throw out", that which is not there in S^3 in the first place.

[Jochen]

You've conveniently ignored the following argument which debunked that claim already. It is not always possible to reconstruct a joint PD from experimental data measured in pairs, even if the model is local realistic!

This is wrong: I have given an explicit construction such that for any LHV-model, you can construct a joint PD.

You ignored the argument. I just showed you that you are wrong, where specifically does the argument fail. Please be very specific.

I've already addressed that argument. That follows from the fact that both are drawn from the same probability distribution, which yields the same correlations. And yes, this does entail that (asymptotically) for two equally long measurement sequences, there will be as many instances of +1 and -1 in both sequences; this is the same as saying that for a coin with some probability of yielding heads p, there will approximately p*number of trials heads in a long enough measurement sequence, and (1-p)*number of trials tails. This, too, will yield the same amount of heads versus tails in two different runs.

You just provided two different QM predictions for the same question. Maybe you haven't realized yet that your previous answer was:

No. I've told you the QM predictions for a two-particle system in the state , and the QM predictions for a four-particle system in the state . These are different systems; they produce different predictions. This is not a fine point, and if it's lost on you, I would humbly suggest you consult an intro-QM textbook.

[Jochen]

There are no zero outcomes either in my theoretical model or in its simulation. They simply do not exist. One cannot detect that which is not there in the first place!

So, what happens in the cases where A(a,e,s) = 0?

[minkwe]

I've already addressed that argument. That follows from the fact that both are drawn from the same probability distribution, which yields the same correlations. And yes, this does entail that (asymptotically) for two equally long measurement sequences, there will be as many instances of +1 and -1 in both sequences; this is the same as saying that for a coin with some probability of yielding heads p, there will approximately p*number of trials heads in a long enough measurement sequence, and (1-p)*number of trials tails. This, too, will yield the same amount of heads versus tails in two different runs.

Please read carefully, this argument has been thoroughly debunked in this post viewtopic.php?f=6&t=168&start=200#p4709 and this one viewtopic.php?f=6&t=168&start=160#p4662

You just provided two different QM predictions for the same question. Maybe you haven't realized yet that your previous answer was:

No. I've told you the QM predictions for a two-particle system in the state , and the QM predictions for a four-particle system in the state . These are different systems; they produce different predictions. This is not a fine point, and if it's lost on you, I would humbly suggest you consult an intro-QM textbook.

Again please read carefully. How do you obtain 4 paired correlations which are not independent, from a single two particle system? Don't you see that the 4 paired correlations in the CHSH expression are not independent but the QM predictions you now claim are the correct ones for the CHSH are completely independent! Don't you see that what you are now providing could not possibly be the correct correlations for the CHSH scenario!?

If this point is lost on you, I would humbly suggest you relearn logic.