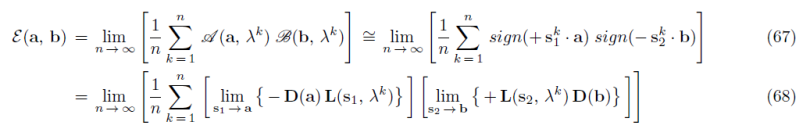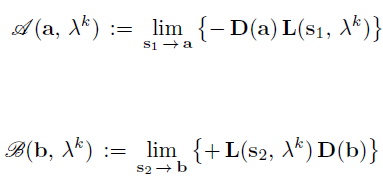EPR-Bell is proof that we live in a quaternionic 3-sphere

[Joy Christian]

***
Hi Everyone,

I have revised my local causality paper, adding some discussion about how the sign flips from AB = -1 to AB = +1 in the EPR-Bohm type experiments are induced by the twist in the U(1) bundle over S^2 constituting the 3-sphere. To me the strong correlations we observe in Nature are a proof that we live in a quaternionic 3-sphere.

Below I have reproduced the new paragraphs in the revised paper for your convenience. As some of you know, I have also proposed a macroscopic experiment to test the hypothesis that we live in a quaternionic 3-sphere rather than a flat Euclidean 3-space. I have also reproduced an essential page from a Report by Eguchi, Gilkey, and Hanson, which discusses the U(1) bundle over S^2 I have used in my revised paper. Needless to say, this is all pretty well known stuff, for those who know it well.







The following discussion is from page 272 of T. Eguchi, P. B. Gilkey, and A. J. Hanson, Physics Reports, volume 66, No. 6, pp 213-393 (1980).


***

[Joy Christian]

***
In Appendix 1, page 20, of this paper I have illustrated how the sign flips AB = -1 to +1 comes about using a toy model of a 1-sided Mobius world of 2D Alice and Bob.

Needless to say, the toy model is not to be taken too seriously. It is for an intuitive entertainment only.



(cf. the logo of our Research Centre: http://einstein-physics.org/)

***

[Joy Christian]

***
Actually, I pointed out the crucial role played by the Hopf fibration of the 3-sphere in the case of Aspect-type experiments using photon polarizations back in 2011: https://arxiv.org/abs/1106.0748. That was five years ago. Hopf fibration of the 3-sphere is one of the transparent ways to understand the EPR-Bohm correlations.



***

[Joy Christian]

***
The following figure is from my paper published in the IJTP last year: http://link.springer.com/article/10.100 ... 014-2412-2.

The published paper is behind the paywall, but the pre-print is freely available on the arXiv: https://arxiv.org/abs/1211.0784.



This figure depicts the effect of the sign changes from AB = -1 to +1 discussed above by comparing the respective geodesics on the group manifolds SU(2) versus SO(3).

There was a serious and sustained attempt by the usual suspects, the usual Bell-fanatics, to have it retracted from IJTP. But on that occasion they failed their crusade.

PS: It is worth noting that Bell-crusaders are unable to prove their "theorem." My challenge to Bell's "theorem" remains uncontested: viewtopic.php?f=6&t=275#p6681.

***

[thray]

HI Joy,

Thought the following might be relevant. Submitted to Scott A's blog on date noted, never got out of moderation:

Thomas H Ray Says: Your comment is awaiting moderation.
Comment #63 May 11th, 2012 at 7:22 am
Bram Cohen #8

As unlikely as it is that any of my comments will survive moderation, I will persist anyway:

“A neat trick is to make it so that this thing which appears to be right next to you is actually right next to you, which is a very handy way of implementing the projective plane, and also a good way of understanding the oddball property the projective plane has that when you wander off into the distance until you come back to where you started you’ve flipped handedness.”

That’s identical to a Mobius band type transformation or the Dirac belt trick. Why it doesn’t apply to Joy’s model as other than analogy is proven by some elementary topology:

RPP is nonorientable. The orientability of Joy’s model implies that the measurement function is nondegenerate near the singularity. What this means for a model in which parallelized S^3 is one of infinite possible Hopf fibrations is that the function bounded in space (by parallelized S^7) is unbounded in time. It can’t be otherwise, because the measurement function is continuous from the topological initial condition for which the input argument — a.b is anticorrelated with the output of a measurement made in a bounded length of time.

This explains why choices of A and B measurement directions on R^3 don’t have the feature of classical time reverse symmetry, and why continuous measurement functions do. I.e., as Cristi #12 said, “By removing one point from the 3-sphere you get, topologically, the 3-Euclidean space. There is only one circle from the Hopf fibration which is broken, and it is broken in just one point, which is at infinite. All other circles remain “entangled”. So it is hard to believe Joy’s claim that the 3-sphere is so magic as compared to the 3-Euclidean space.”

This is true. You get entanglement (i.e. quantum entanglement described by a probabilistic wave function) only by ignoring the point at infinity. It isn’t (parallelized) S^3 that Joy claims is “magic,” however; the magic is the fully generalized topology of S^7. This is the limit of spheres (of the set S^0, S^1, S^3, S^7) admitting a division algebra (8-dimension, octonionic); S^3 admits 4-dimension, quaterionic, S^1, the 2-dimension algebra of C and S^0, the 1-dimension R. The complete factorizability of the model is all arithmetically correct.

Because every experimental measure of correlated particle pair properties is performed in a bounded length of time, the measurement is manifestly local. What makes it real is the correspondence between the measure result (click, flash, track, etc.) and proof that the result COULD have been other than it is, i.e., have a reversible trajectory. There is no way to prove this other than by statistical inference allowing a continuous measurement function with classical time reverse symmetry — and that can only happen if the measurement function is nondegenerate near the singularity.

It is accepted in topology that on S^3, the definition 1/0 = oo. Infinity isn’t a number, so one doesn’t say that the illegal arithmetic operation of division by zero is possible. One can say, however, that there are real measures either “side” of infinity that are anticorrelated.

If one allows, as you do, that any physical measurement is restricted to R^3, then one assumes that all measurement functions are degenerate. Since this won’t work for classical (continuous function) physics, the implication is that no deterministic theory of physics is possible. The proof of this, however, is entirely nonconstructive.

[thray]

And other such instance:

Thomas H Ray Says: Your comment is awaiting moderation.
Comment #129 May 14th, 2012 at 9:57 am
Scott # 127

” … my conclusion was that Joy’s papers held up even less well than if I’d merely gone on the absurd title and other ‘indirect’ evidence!”

Yes of course, I understand what your conclusion is based on. The counterpoint, though, is a question of whether there is an alternative to the nonconstructive proof of Bell’s theorem. If there is, then one has to question the experimental basis for validating its correspondence to physical reality. If Joy had not proposed such a correspondence, I would never have gotten into this kerfuffle. I would be satisfied to let Bell’s theorem stand as the mathematical description of a probabilistic, observer-created world, and Joy’s mathematical model would be a curiosity without physical application.

I am neither physicist nor computer scientist. I do grasp, though, the difference between the discrete numerical implementation of a model, and a real continuous measurement function. I don’t think the latter has been given a fair hearing, and I do think that your impossibility argument A(a,λ) B(b,λ) ≠ -λ^2 does not apply. A and B lambdas being independent variables obviates this ordering, because there is no reversible time parameter, as a continuous function requires; i.e., A and B in Joy’s model are linearly ordered into independent and reversible time intervals by the input argument. They can’t be forced into a static 2-dimension relation without assuming a Hilbert space simultaneity which begs the probabilistic measure space of standard QM (measurements made “at a time”).

Joy’s model is classical. It never trades real deterministic measure values for a probabilistic outcome. The predicted measure values are discrete, though the measurement function is continuous (from the input argument -a.b). The only reason this would sound cranky is our entrained familiarity with the calculating tools of standard quantum mechanics.

[Joy Christian]

***
Thanks, Tom.

Aaronson also blocked many of my rebuttals from his sordid blog because they would have been too uncomfortable for him. They would have exposed his dogmatism, ignorance, and hypocrisy. Instead of honestly engaging with my rebuttals openly, he systematically blocked them and resorted to hiding behind insults and treachery.

Anyone who still believes in Bell's "theorem" has to prove it first, to prove that they are engaged in science. Here is their chance: viewtopic.php?f=6&t=275#p6681.

***

[Joy Christian]

***
Thanks, Tom.

Aaronson also blocked many of my rebuttals from his sordid blog because they would have been too uncomfortable for him. They would have exposed his dogmatism, ignorance, and hypocrisy. Instead of honestly engaging with my rebuttals openly, he systematically blocked them and resorted to hiding behind insults and treachery.

Anyone who still believes in Bell's "theorem" has to prove it first, to prove that they are engaged in science. Here is their chance: viewtopic.php?f=6&t=275#p6681.

***

For the record, Aaronson not only systematically blocked my posts, but also of anyone who posted in support of my views --- like the posts by Fred, Michel, and Tom.

***

[FrediFizzx]

Just posted this reply on Retraction Watch and is waiting moderation.

You did not respond to my point that there is a simple direct proof that Christian’s assumptions imply that E(a, b) = -1 for all a and b: namely via the equalities A(a, lambda) = – B(b, lambda) = lambda = +/-1 for all a and b, see definitions (54) and (55). No amount of nifty (but correct) mathematical tricks can ever get a different result.

What would the A and B functions be for QM to produce +/- 1 outcomes? They would certainly have to be something like Joy’s A and B functions. So does that mean that quantum mechanics also predicts -1 as a result? No! The -a.b prediction from quantum mechanics for an EPR-Bohm scenario is derived by a probabilistic method and is NOT simply A*B. Bottom line is that the predictions for a theory are calculated in a different way from how experimental results are calculated. So it is quite a mystery as to why you are rejecting that.

[Joy Christian]

Just posted this reply on Retraction Watch and is waiting moderation.

You did not respond to my point that there is a simple direct proof that Christian’s assumptions imply that E(a, b) = -1 for all a and b: namely via the equalities A(a, lambda) = – B(b, lambda) = lambda = +/-1 for all a and b, see definitions (54) and (55). No amount of nifty (but correct) mathematical tricks can ever get a different result.

Well, this is Gill's main beef for quite some time, and you and I have addressed it literally hundreds of times, in many different ways, starting from my very first reply to him in this paper: https://arxiv.org/abs/1203.2529 [see eq. (42)]. The point he keeps missing is that the functions A and B in my model represent scalar points of a quaternionic 3-sphere, something that I have endlessly emphasised, literally thousands of times. It is then disingenuous of him to claim that E(a,b) = -1 for all a and b.

My assumptions by no means "imply that E(a, b) = -1 for all a and b." Nor do they "imply A(a, lambda) = – B(b, lambda) = lambda." That is pure BS, and Gill knows that:

viewtopic.php?f=6&t=271#p6808

But let me address the issue again in a different way. Jay asked me privately today whether I can prove that conservation of spin-0 momentum is violated if we insist on E(a, b) = -1 for all a and b. The answer is, Yes. If we insist on E(a, b) = -1 for all a and b, then my eq. (68) shown below implies that – (s_1 . s_1) (s_2 . s_2) = -1:



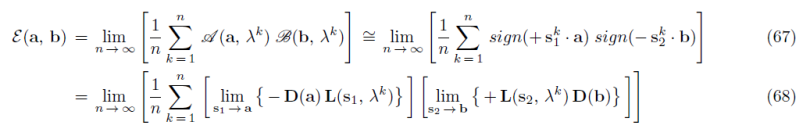
Which in turn implies that ||s_1||^2 ||s_2||^2 = 1, and that implies ||s_1|| = 1 / ||s_2||, which violates of the conservation of spin-0 angular momentum. If we increase the magnitude of s_1, then the magnitude of s_2 decreases, and vice versa. Whereas the conservation of spin-0 momentum requires that ||s_1|| = ||s_2||.

This explicitly shows, as I have stressed hundreds of times before, that there is no way of obtaining E(a, b) = -1 for all a and b without violating conservation of spin.

***

[FrediFizzx]

That is all good but approaching it from a different direction shows Gill is completely wrong also. A and B functions that give +/- 1 outcomes are not possible for QM and still have the -a.b prediction. It can only be done using hidden variables. QM does not use A*B for its correlation prediction so it is absurd to think that a LHV model should have to also.

[Joy Christian]

That is all good but approaching it from a different direction shows Gill is completely wrong also. A and B functions that give +/- 1 outcomes are not possible for QM and still have the -a.b prediction. It can only be done using hidden variables. QM does not use A*B for its correlation prediction so it is absurd to think that a LHV model should have to also.

Bell's point was that no LHV producing A, B = +/-1 can also produce E(a, b) = -a.b. QM is not required to produce +/-1 using A and B because it is not a LHV theory.

As far as Gill's comments above are concerned, he is deliberately misleading the readers. My functions (54), (55) producing A = +/-1 and B = +/-1 are the following:



But Gill writes my functions as A = +lambda and B = -lambda to deliberately mislead the readers. He knows full well that nearly 95% of physicists are not well versed in the Bell literature so he will get away with such a gross misrepresentation, and he has. Alternatively Gill is literally stupid to confuse the measurement outcomes A and B with the hidden variable lambda when he writes A = +lambda and B = -lambda. At the least, his measurement functions are a gross distortion, or a straw-man.

***

[FrediFizzx]

Bell's point was that no LHV producing A, B = +/-1 can also produce E(a, b) = -a.b. QM is not required to produce +/-1 using A and B because it is not a LHV theory.

It may not be required by Bell but who cares about that? If you are modeling a typical quantum EPR experiment, you have to produce +/- 1 outcomes at stations A and B. My whole point is that QM can't do it without hidden variables. Bell was making a direct comparison of LHV models to QM, so it is pretty stupid to require LHV models to produce +/-1 outcomes when QM can't do it (can't model a quantum experiment completely) and give the QM prediction as a result. Bell was wrong so no one needs to have to play by his "rules". IOW, your A and B functions don't have produce +/- 1 outcomes to match QM's prediction. All you really need is the correlation calculation for the prediction. But your A and B functions produce +/- 1 outcomes anyways so that is a plus. So Gill's objections don't hold water no matter which way you look at it.

IOW, you could just take all the +/- 1 stuff off eqs. (54) and (55) and your model still gives the same prediction as QM. And you could drop the limits off A and B. They are not required in that case. That for sure kills Gill's -1 result complaint since there is no +/-1 outcomes to deal with. A does not necessarily equal lambda, etc. Basically your model is an explanation for the results of the QM experiments in a classical local-realistic way. Period.
.

[Heinera]

Re the above, here is a question for Fred: What do you think is the definition of a "local realistic" theory? Local should be obvious, so what it your take on "realistic"?

[FrediFizzx]

Re the above, here is a question for Fred: What do you think is the definition of a "local realistic" theory? Local should be obvious, so what it your take on "realistic"?

In the case of the EPR-Bohm scenario, the results of theory are predictable without using probability. That is exactly what Joy's model does. It predicts -a.b as the result without using probability.

But I know what you are thinking. If you know lambda, you can predict the individual outcomes at A and B. That is a Bell BS trap.

[Heinera]

Re the above, here is a question for Fred: What do you think is the definition of a "local realistic" theory? Local should be obvious, so what it your take on "realistic"?

In the case of the EPR-Bohm scenario, the results of theory are predictable without using probability.

Ok, but:

But I know what you are thinking. If you know lambda, you can predict the individual outcomes at A and B. That is a Bell BS trap.

So, that you can predict the individual outcomes at A and B without using probability is just BS? So "realism" is just BS?

[Joy Christian]

***
Heinera,

If you know it all, then why don't you prove Bell's "theorem" for us? Here is my challenge again: viewtopic.php?f=6&t=275#p6681. Put up or shut up.

***

[FrediFizzx]

Re the above, here is a question for Fred: What do you think is the definition of a "local realistic" theory? Local should be obvious, so what it your take on "realistic"?

In the case of the EPR-Bohm scenario, the results of theory are predictable without using probability.

Ok, but:

But I know what you are thinking. If you know lambda, you can predict the individual outcomes at A and B. That is a Bell BS trap.

So, that you can predict the individual outcomes at A and B without using probability is just BS? So "realism" is just BS?

For you it apparently is BS since you fail to appreciate the whole scenario. The theory doesn't necessarily have to predict individual outcomes in an EPR-Bohm scenario. That is a stupid restriction that Bell erroneously created. To correctly match QM, the theory only needs to correctly predict the final result of many trials without probability. And the comparison of LHV to QM is what Bell's theory is all about. Fair is fair and Bell's restrictions are not fair so his theory is false.

[Heinera]

Well, if you cannot "predict individual outcomes", but can only "predict the final result of many trials", that is the very definition of probabilistic reasoning.

[FrediFizzx]

Well, if you cannot "predict individual outcomes", but can only "predict the final result of many trials", that is the very definition of probabilistic reasoning.

Show us where the probability is in Joy's model.

And I only said the prediction for individual outcomes are not required to properly match LHV to QM. That is another place where Bell failed.